MATHÉMATIQUES
Proportion et évolution en pourcentage
Sommaire
1) La proportion
La proportion est une relation mathématique entre deux ou plusieurs quantités qui exprime comment elles se rapportent les unes aux autres.
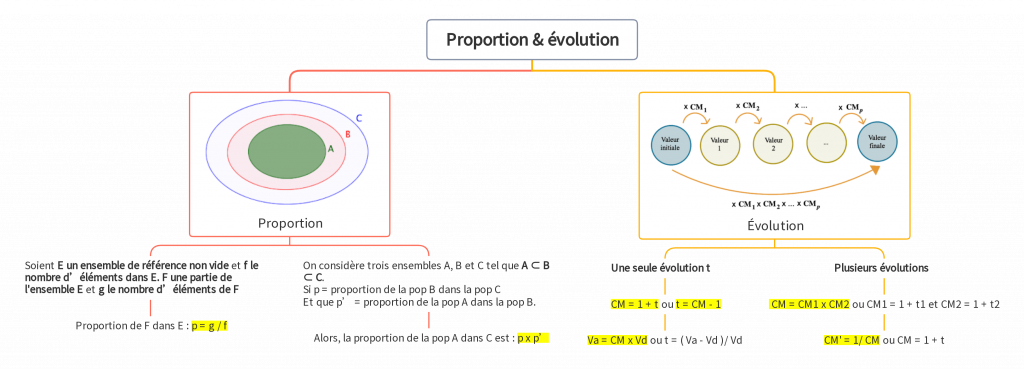
DÉFINITION : Soient E un ensemble de référence non vide et f le nombre d’éléments dans E. F, une partie de l’ensemble E et g le nombre d’éléments de F.
On appelle proportion p de F dans E le réel p = g / f
Exemple : Si une classe de 25 élèves a 15 filles, on peut utiliser la proportion pour déterminer la proportion de garçons dans la classe. On sait que la proportion de filles est de 15/25, soit 0,6. Pour trouver la proportion de garçons, on soustrait cette valeur de 1 :
1 – 0,6 = 0,4. On en conclut que la proportion de garçons dans la classe est de 0,4 ou 40%.
a – Proportion de proportion
On considère trois ensembles A, B et C tel que A ⊂ B ⊂ C .
Si p = proportion de la pop B dans la pop C
Et que p’ = proportion de la pop A dans la pop B.
Alors, la proportion de la pop A dans C est : p x p’
Exemple : En 2023, le lycée accueille beaucoup de nouveaux élèves. Parmi ces élèves, 30 % sont inscrits en seconde.
Parmi ces élèves en seconde, 15 % sont en seconde 3.
Ici, la pop C est le lycée, la pop B est les secondes et la pop A est les secondes 3.
pour connaître la proportion de secondes 3 dans le lycée ( donc de A dans C )
On applique la formule : 15 % x 30% = 0,045 soit 4,5 % .
On a donc 4,5% des nouveaux élèves qui se trouvent en seconde 3.
| Lorsqu’une proportion de proportion est donné en pourcentage, on parle de pourcentage de pourcentage |
2) Évolution en pourcentage
a – Variation absolue et relative
DÉFINITION : La variation absolue est la différence entre deux valeurs. Elle mesure le changement absolu dans une quantité. Elle est alors exprimé sous la forme suivante : Va – Vd
avec Va = valeur d’arrivé et Vd = valeur de départ
Exemple: si le prix d’un produit est passé de 10€ à 12€, la variation absolue est de 2€.
(On a fait : 12 – 10)
DÉFINITION : La variation relative est la variation exprimée en pourcentage de la valeur initiale. Elle mesure le changement relatif dans une quantité. Elle est exprimé sous la forme : (Va-Vd) / Vd x 100
Exemple : Si le prix d’un produit est passé de 10€ à 12€, la variation relative est de 20%. On calcule cela en divisant la variation absolue par la valeur initiale et en multipliant par 100 : (12 – 10) / 10 x 100 = 20%.
b – Coefficient multiplicateur
La variation relative est aussi appelée taux d’évolution (t)
Il est nécessaire pour faire passer la valeur de départ à la valeur d’arrivée.
En effet, le coefficient multiplicateur est donné par : CM = (1+t)
Le coefficient multiplicateur est le coefficient qui multiplie la valeur de départ pour donner la valeur d’arrivée : Va = CM x Vd ou Va = (1+t)Vd
Le coefficient multiplicateur est utilisé pour calculer la variation relative d’une quantité.
Exemple: si le prix d’un produit a augmenté de 20%, le coefficient multiplicateur est de 1,2
(1+t => 1+20%). Pour trouver le nouveau prix après l’augmentation, on multiplie le prix initial par le coefficient multiplicateur.
Supposons qu’un produit coûte initialement 100€. Si le prix augmente de 20%, le nouveau prix sera :
Nouveau prix = 100€ x 1,2 = 120€
ici, 100€ est la valeur de départ et 1,2 le coefficient multiplicateur CM avec t = 20%
c) Évolution successive
Comme on l’a vu, pour passer d’une valeur de départ à une valeur d’arrivée il faut multiplier la Va par le coefficient multiplicateur.
Lorsqu’il y a évolution successive, on parle de coefficient multiplicateur global
On va multiplier le CM1 ( Q0 => Q1 ) avec le CM2 ( Q1 => Q2) ce qui va nous donner le CMglobal ( Q0 => Q2)
On a donc: CMglobal = CM1 x CM2.
d) Évolution réciproque
Pour passer de la valeur de départ à la valeur d’arrivée, on a le coefficient multiplicateur.
On peut à présent partir de la valeur d’arrivée pour obtenir la valeur de départ grâce au coefficient multiplicateur réciproque.
Le coefficient multiplicateur réciproque ( CM’) est l’inverse du coefficient multiplicateur (CM)
On a donc: CM’ = 1/CM
exemple: si le prix d’un produit a augmenté de 25%, le coefficient multiplicateur est de 1,25. Pour trouver la variation inverse, c’est-à-dire la diminution relative, on utilise la formule CM’ = 1/CM, où CM est le coefficient multiplicateur initial.
Supposons qu’un produit coûte initialement 100€ et que le prix augmente de 25%, le nouveau prix sera :
Nouveau prix = 100€ x 1,25 = 125€
Pour calculer la variation inverse, on utilise la formule CM’ = 1/CM :
CM’ = 1/1,25 = 0,8
Ainsi, lorsqu’on fait 125€ x 0,8 on trouve bien 100€
Formules:
Formules de proportions
p = g / f ( voir la correspondance )
pop A dans pop C = p x p’ (voir l’exemple)
Variation absolue et relative
variation absolue = Va-Vd
Variation relative = t = (Va-Vd) / Vd x 100
Coefficient multiplicateur
CM = (1+t)
Va = CM x Vd ou Va = (1+t)Vd
évolution successives
CMglobal = CM1 x CM2 (voir démo)
Évolution réciproque
CM’ = 1/CM
Vidéo :
Carte mentale: